2次元のAdaptive Dynamics理論
[前のページ:1次元の方向進化と進化的分岐点の解析]
[次のページ:2次元の進化的分岐線の解析]
2次元形質空間のAdaptive Dynamicsは概ね1次元の場合の自然な拡張ですが、2次元では回転の自由度があるため、収束安定性が少し違います.
Table of Contents
1 仮定
- 2次元形質空間s = (x, y)T
- 突然変異は希で小規模(⇒個体数動態は常にほぼ平衡状態)
2 侵入適応度(invasion fitness)
2.1 定義
侵入適応度は1次元の場合と同じで、以下のように定義されます.
野生型s°に対する変異型野生型s’の侵入適応度f(s’, s°):単型の野生型s°からなる集団の個体数密度n°が平衡個体数密度n̂にあるとき、出現した変異型s’の初期増加率.
すなわち変異型s’の個体数密度をn’として
すなわち変異型s’の個体数密度をn’として
野生型は平衡密度にあるので全てのs°についてf(s°, s°) = 0です.また、f(s’, s°)を野生型s°の存在下における適応度地形とみなすことができます。
2.2 形質置換連鎖(trait substitution sequence)
形質置換連鎖も1次元の場合と同じなので説明を省きます。
3 方向進化(directional evolution)
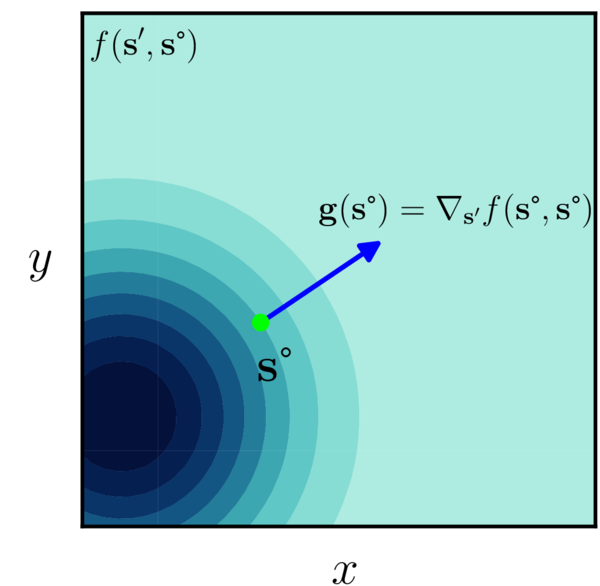
集団の方向進化は野生型(あるいは平均表現型)の位置の適応度勾配(fitness gradient)に比例します(Fig.1):
(2) g(s°) = ⎛⎜⎝
gx(s°)
gy(s°)
⎞⎟⎠ = ∇s’f(s°, s°) = ⎛⎜⎝
⎡⎣(∂f(s’, s°))/(∂x’)⎤⎦x’ = x°
⎡⎣(∂f(s’, s°))/(∂y’)⎤⎦x’ = x°
⎞⎟⎠.
方向進化の期待速度は以下の式により近似的に与えられます(Dieckmann and Law, 1996):
進化の方向は量的遺伝学におけるLandeの式やPrice方程式と同じですが、速さは異なります.
4 進化的特異点
4.1 進化的特異性(evolutionary singularity)
野生型がそこに居ると方向性選択が0になる点を進化的特異点(evolutionarily singular point)と呼びます.すなわち、点sが進化的特異点であるとき、
(5) g = g(s) = 0.
4.2 進化的特異点の分類
4.2.1 収束安定性(convergence stability)
進化的特異点sが以下の条件を満たす時、sを強収束安定点(strongly convergence stable point)と呼びます(Leimar, 2005, 2009):
(6) C = ⎛⎜⎝
Cxx
Cxy
Cyx
Cyy
⎞⎟⎠ = ⎛⎜⎝
(∂[g(s°)]T)/(∂x)
(∂[g(s°)]T)/(∂y)
⎞⎟⎠s° = s = ⎛⎜⎝
(∂gx(s°))/(∂x°)
(∂gy(s°))/(∂x°)
(∂gx(s°))/(∂y°)
(∂gy(s°))/(∂y°)
⎞⎟⎠s° = s
の対称成分(1)/(2)[ C + CT]の固有値が全て負.このCは
(7) ∇s’∇Ts’ f(s, s) = ⎛⎜⎝
(∂2f(s’, s°))/(∂x’2)
(∂2f(s’, s°))/(∂x’∂y’)
(∂2f(s’, s°))/(∂x’∂y’)
(∂2f(s’, s°))/(∂y’2)
⎞⎟⎠ s’ = s° = s
(8) ∇s°∇Ts’ f(s, s) = ⎛⎜⎝
(∂2f(s’, s))/(∂x°∂x’)
(∂2f(s’, s))/(∂x°∂y’)
(∂2f(s’, s))/(∂y°∂x’)
(∂2f(s’, s))/(∂y°∂y’)
⎞⎟⎠s’ = s° = s
を用いて以下のように変形できます.
強収束安定点は、方向進化が式(3)で与えられる単型の集団を、Vが正則行列である限り引き寄せるという強い性質を持ちます。
4.2.2 進化的安定性(evolutionarily stability)
進化的特異点sが以下の条件を満たす時、sを進化的安定点(Maynard Smith and Price, 1973)と呼びます.
(10) D = ∇s’∇Ts’ f(s, s)
の固有値が全て正.この条件は、集団がsに居るときに、周囲の適応度地形が山形になっていることに対応します.2つとも負の場合は盆地、1つが正で1つが負の場合は鞍点です.
4.2.3 相互侵入可能性(mutual invasivility)
進化的特異点sが以下の条件を満たす時、sを相互侵入可能(Prout, 1968)であると表現します.
の対称成分が少なくとも1つの負の固有値を持つ.
5 進化的分岐点(evolutionary branching point)
- 候補点付近の単型の無性生殖集団は、その点へ方向進化し、Dの最大固有値の固有ベクトル方向に分岐します。
- これらの条件を満たす「進化的分岐点の候補」が付近の単型集団の進化的分岐を保証するかどうかは形質置換連鎖の枠組みでは証明されていません。しかしGeritz et al. (2016)は、候補点付近で複数の表現型が共存する場合のそれらの方向進化をLandeの式で近似的に記述することにより、進化的分岐が達成されることを証明しました。従っておそらくは、進化的分岐の候補点は進化的分岐を保証すると予想されます。少なくとも進化動態の数値計算においては、進化的分岐を促さない候補点は見つかっていません。
- 候補点の条件は3次元以上の場合も同様ですが、全ての候補点が進化的分岐を促すかどうかは、3次元以上ではまだ証明されていませんので数値計算の併用が必要です。
6 適用例:資源競争モデル
6.1 個体数動態モデル
ここでもロトカ・ヴォルテラの資源競争モデルを考えます.
このモデルはMacArthur-Levins資源競争モデルと呼ばれています.
6.2 侵入適応度
単型s°の集団を考えると、その密度n°の動態は式(12)を用いて以下のようになります.
従ってその平衡密度はn̂° = K(s°)です.変異型s’が出現したとき、その密度の動態は式(23)を用いて以下のようになります.
従って侵入適応度は以下のようになります.
(20) f(s’, s°) = limn’ → 0⎡⎣(1)/(n’)(dn’)/(dt)⎤⎦n° = n̂° = limn’ → 0⎡⎣1 − (n’ + α(s’ − s°)K(s°))/(K(s’))⎤⎦ = 1 − (α(s’ − s°)K(s°))/(K(s’)).
6.3 方向進化
g(s°)
=
∇s’f(s°, s°) = ∇lnK(s°)
=
∇⎡⎣ − (|s°|2)/(2σ2K)⎤⎦(s°)
=
− σ − 2Ks°
従って、進化的特異点s° = 0が存在する.s°において、
であるからこの点は強収束安定点.さらに、
D
=
∇s’∇Ts’ f(s, s)
=
− ∇∇Tα(0) + ∇∇TlnK(s) + ∇lnK(s)∇TlnK(s)
=
− ∇∇Tα(0) + ∇∇TlnK(s)
=
[σ − 2α − σ − 2K]⎛⎜⎝
1
0
0
1
⎞⎟⎠
従って、σK > σαのとき、s = 0は進化的分岐点の候補である.(σK < σαのときは収束安定な進化的安定点.)